As I said in this blog’s introductive post, I will publish presentation, that are blog posts in which I will expose research articles or specific fields of research. This article is the first of the series and is about Xu et al. article: The generalized Shockley-Queisser limit for nanostructured solar cells, Sci. Rep. As I wrote last week, the Shockley-Queisser theory limits the efficiency of solar cells. In this article, we will discuss these phenomena, in relation to Xu et al. article.

How to measure a solar cell’s performances?

For a good understanding of the Shockley-Queisser limit, we first need to define the main figures PV scientists are working with. These figures allow us to compare different solar cells.

Measuring a solar cell is usually done by scanning a voltage and measuring the current response under simulated illumination. Typical solar cells have a response as shown in this figure:

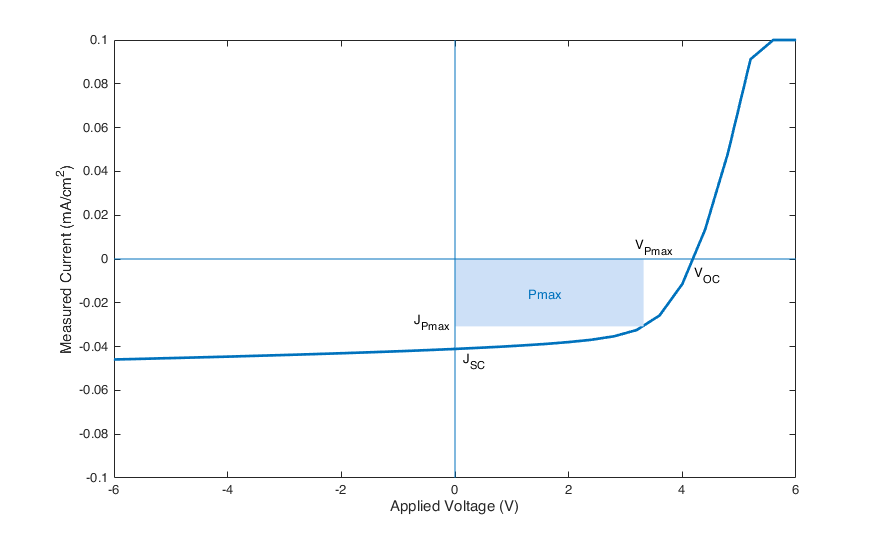
Some data are easily understandable: V_OC is the open circuit current, the maximum voltage the cell will supply. The short circuit current J_SC is the maximum current at zero resistance load.

Pmax is the maximum power the cell can deliver, defined by Pmax = V_Pmax × J_Pmax. Hence we can define the Fill Factor FF:

FF = Pmax /(V_OC × J_SC)

The Fill Factor compares the maximum power with the maximum current and voltage. It is always comprised between 0 and 1 and gives the information about how large the maximum power is in comparison with these two parameters.

Therefore, we define the Power Conversion Efficiency as the ratio of generated electric power and incoming light power:

PCE = Pmax / P_light = I_SC×V_OC×FF/P_light

Those parameters allow us to compare the efficiencies of different solar cells, independently of their sizes. When we talk about the efficiency of a solar cell, we always mean the Power Conversion Efficiency.

Theoretical limits for solar conversion

In a classic PN junction solar cell, the conversion of light into energy is based on the photoelectric effect. It is actually an interaction between an electromagnetic wave and matter, that can be modelled as atom chains, metals, semiconductors or dielectrics. One can picture the problem with Hamiltonians in a realistic potential. In that way, Shockley and Queisser discovered a mismatch between absorption and emission angles. In their 1961 article, they set a balance between incoming photon flux and the emission of other radiation. The calculus is based on a model in which the recombination of a hole-electron-pair is radiative. It is the main source of losses.

They make the assumption that solar cells and the sun behave as black bodies. For a planar solar cell, they compute the maximum efficiency that is found to be 30% for a 1.1eV gap. The model of a planar solar cell is of paramount importance: it is considered that the photons hit a planar surface without any delay or difference.

Considering this hypothesis, one can wonder whether nanostructured solar cells (that cannot be considered as planar) behave with the same law or not. Xu et al. proved the Shockley-Queisser limit efficiency was still valid and proposed a model to adapt it.

Is the Shockley-Queisser limit still valid for third generation PV?

The main hypothesis of the Shockley-Queisser model is that photon ram a planar surface, restricting the maximum power conversion efficiency. A third-generation technology allows us to consider more photons, called Concentrated PV. In fact, a concentration device — like an optical lens or a parabolic mirror — is put above the cell, concentrating more photons upon it. Hence the photons hit the surface with a multitude of different angles. It boosts the efficiency of the considered solar cell. In this case, it is easy to understand that only one hypothesis that changes, expanding the PCE of the concentrator-solar cell device without changing the equations established by Shockley and Queisser in 1961.

Now consider a solar cell without any concentration device but with a structure that is not planar and that is composed of nanostructures. Because of the roughness of the surface, there is also a multitude of angles with which the photon can hit the surface. It allows magnification of the Power Conversion Efficiency the same way concentrated devices work.

Moreover, Xu et al. found that the emission angle is much closer to the acceptance angle for nanostructured devices. Then the entropy generated by this mismatch is lowered resulting in a voltage improvement. For this reason, Nanostructured solar cells have an efficiency limit of about 42%. I find the understanding of this phenomenon of outstanding significance for the improvement of high-efficiency solar cells.

As a conclusion, if the Shockley-Queisser limit seems to minimize the maximum efficiency of a solar cell, the article from Xu et al. shows that third generation photovoltaic technologies found ways to subvert it to boost it. In this example, the understanding of the limiting phenomena helped scientists to find ways to overcome it. That is what I find really interesting.