Less than a month ago, president Donald Trump took the outrageous decision to get out the Paris Agreement. Climate change is real. Climate change is disastrous for our lives, and not only for our children’s and grandchildren’s as we used to say. The Paris agreement aims at limiting global warming below +2°C.

Renewable energies

According to Pye et al. (Nature Energy, 2017), the only way to meet the agreement is switching globally from now on to renewable energies. To do so, there are different sources of energy: solar, wind, waves, tidal… The fact is that we currently need a bit less than 20TW of energy. Scientists predict we will need 30TW in 2050 and 50TW in 2100. Let’s put these figures in relation with available sources of renewable energy. Biomass is can produce from 5 to 7TW. Hydroelectric can produce up to 1.2TW. Geothermal energy is worth 1.9TW, tide: 0.7 TW and wind: 14TW. Solar energy received at earth surface accounts for 10⁵TW. Therefore solar energy can feed the demand entirely. I will focus on the way to produce electricity from solar energy.

First Generation Solar Cells

In 1921, Albert Einstein received the Nobel Prize of physics for the discovery of the law of the photoelectric effect. This effect describes the emission of electrons when the light is absorbed onto a material. It is the basis of the first generation of solar cells that still represent 90% of the market.

This technology is based on a crystalline semiconductor (silicon). One layer of crystalline n-doped semiconductor (in which a doping agent has been added so that the electron concentration is higher than the holes concentration: it has electrons to give away) is stuck to a layer of crystalline p-doped semiconductor (with higher hole concentration than electrons: it has electrons to be given), creating a P-N junction. Properties of P-N junctions can be well and easily understood using stationary states of the Schödinger Equation but I will not explain it here.

The electrons should be excited from a valence band into a conduction band to produce electricity as a current. These bands are separated by a gap. It means that, for a photon to excite an electron into a higher energy state, the energy must be greater than or equal to the energy of the gap. The energy can be tuned when doping differently the two regions. It means first generation solar cells have a broad spectral absorption range. However, if a photon has an energy higher than the gap, the extra energy is wasted as heat. It defines a limit in the yield, known as the Shockley-Queisser limit. Moreover, producing crystalline silicon requires expensive manufacturing technologies.

Why do we need other technologies?

Silicon is a pretty good technology. However, a huge amount of energy is needed for the production of solar cells and in their use to produce energy. That is why we need to take into account other parameters: energy needed for preparation, energy output, lifetime, availability and costs to understand whether the technology can be used for 100% of the energy production or not. For a clear demonstration, I will only estimate orders of magnitude.

Photovoltaics is a fast growing business, therefore availability of the technology is a real problem. Let’s say, for example, that we want to replace all the electrical power output of a nuclear power plant with a nominal 1GW production. We use crystalline silicon with a module efficiency η_sc = 0.1, exposed to an average central European insolation Φ_exp = 100W/m².

We assume we need 1mm of silicon to produce a mean absorber thickness of the silicon wafer d_Si = 500µm, (we need another 500µm that accounts for Si powder produced by slicing the ingots), the total volume of silicon is V_Si = 10⁸ × 10⁻³ = 10⁵ m³. The energy needed to produce crystalline silicon wafers is around 1,000 kWh/m², which corresponds to about 100GWh for the 1GW PV plant example. Lifetime of a silicon solar cell is about 30years (τ = 10⁴days), therefore for one 1GW plant, we need a production rate of V_prod = V_Si/τ = 10m³/day and then P_prod = 10 kWh/day = 100kW/day of production. Because the annual production of a 1GW plant is U_prod = 10TWh then it is U_tot = 10¹⁴ Wh over 30 years and yields P = 1GW. Then t_payback = U_tot/P = 10¹⁴ / 10⁹ = 10⁵ h = 10 years. It means the effective production of the solar plant is only 20 years.

Replacing 1GW would require a total module area : A_sc = P / (η_sc · Φ_exp) = 10⁸ m² = 10km×10km = 6miles×6miles.</p>

Now, if we consider we need to replace not only 1 power plant but all earth production. For 30TW (expected needs in 2050), we would need 3·10¹² m² of solar panels, that represents India's area. Would you imagine using such a surface with such an energy payback time (and therefore such a cost)? I don't. That is the reason why I consider we need to find new and emerging technologies for PV devices. That is why scientists have tried designing new materials and new technologies. ### Second Generation Solar Cells A solution towards reducing the cost and the price of active materials is diminishing their quantities in solar cells. That is the principle of Thin Films devices, known as the Second Generation of Solar Cells. This second generation photovoltaic reduces the price per watt by removing the unnecessary materials thereby reducing the cost equation. The use of thin films allows lowering the number of materials without losing efficiency. These solar cells are single junction semiconductors that aim to use fewer materials. The semiconductor of the most used cells is amorphous silicon, CuInGaSe₂ (CIGS), CdTe-CdS or polycrystalline Si on a low-cost substrate. This technology absorbs solar spectrum with greater efficiency than crystalline silicon and uses only 1 to 10µm of active material. However, their conversion efficiency is lower than crystalline silicon. Because Thin Film Solar cells are semitransparent, they can be applied as window glazing for the Building Integrated Photovoltaics (BIPV) market. Nonetheless, there are still many ways to enhance the efficiency of solar cells. This leads us to the third generation. ### Third Generation Solar Cells At the beginning of the 21st century, scientists have tried new techniques to overcome the Shockley-Queisser limit. With this objective begins a true race to design materials able to overcome it. Scientists have tried to optimise charge collection and thereby enhance energy capture. With the discovery of organic materials, solar cells had the potential for low cost and high optical absorption. The use of innovative semiconductors defines the third generation of solar cells. These cells are mostly known under the *Emerging PV* name: * photoelectrochemical cells that produce energy in a process similar to the electrolysis of water; * dye-sensitized solar cells in which the active material is a complex formed by a dye on a highly porous semiconductor material; * organic and polymer solar cells, working with a P-N junction made with an electron donor polymer and a hole donor polymer; * quantum dot solar cells, that use quantum dots as the semiconductor layer; * copper zinc tin sulfide (CZTS) and derivatives, thin film-like technology; * perovskite and kesterite solar cells, in which the semiconductor is a crystalline material. Other techniques allow to surpass the Shockley-Queisser limit: * multijunction cells that are cells composed of many layers with the ability to absorb different energies; * intermediate band cells which have multiple bandgaps to increase their energy; * hot carrier cells that convert the excess energy of above-bandgap photons into electricity; * spectrum conversion that converts the incoming polychromatic sunlight into a narrower distribution. 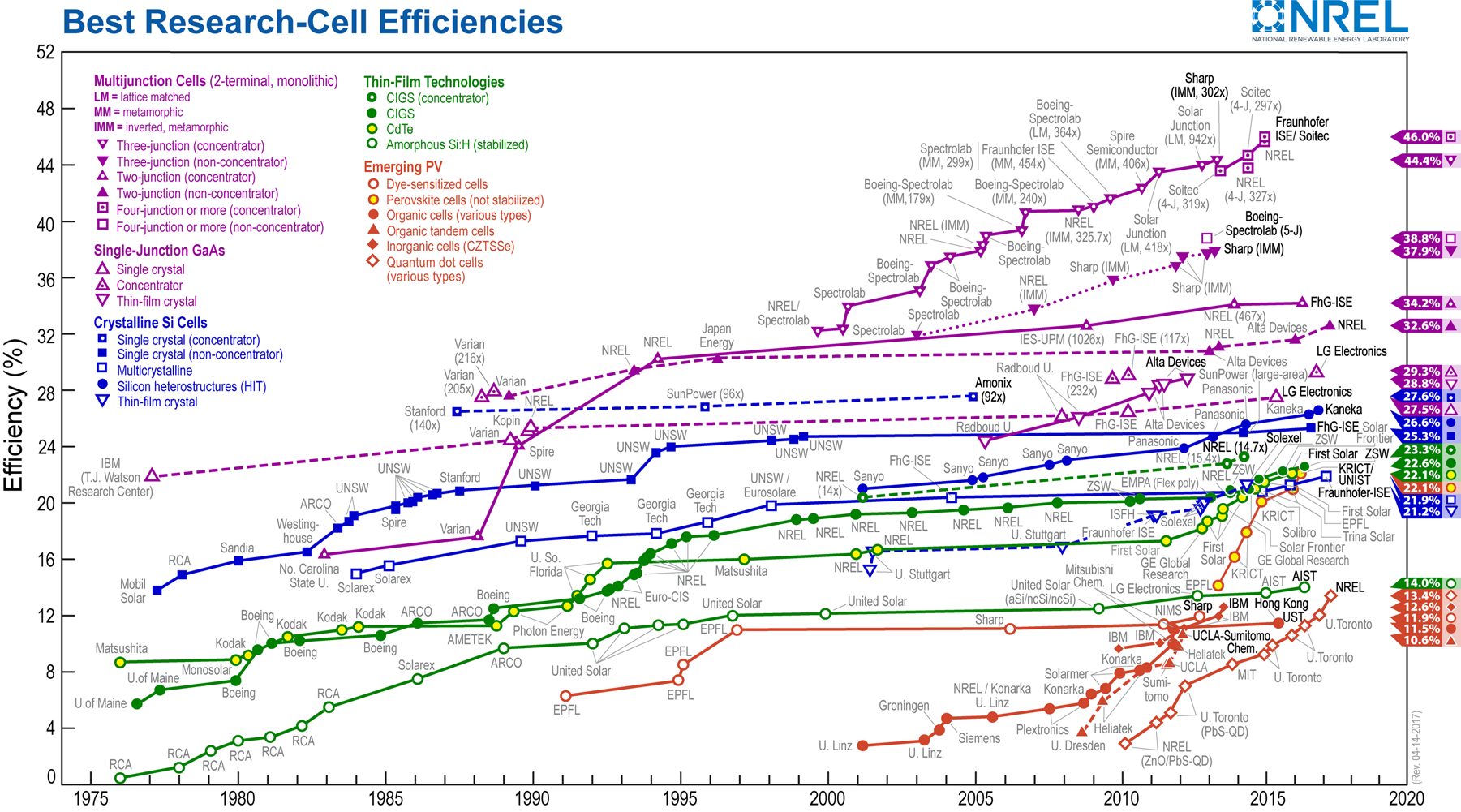### Research evolution This plot shows the highest conversion efficiency for different types of solar cells:

We see on this plot that even if the efficiencies of third generation solar cells (Emerging PV) are lower than current efficiencies of first and second solar cells, the evolution is much faster. Hence this field is of growing interest, I will show it in future articles.