I’m regularly invited to the Journal club in the group of Roman Gorbachev at the University of Manchester. Each week, two of us present a paper each. It is a good occasion to catch up with research we wouldn’t be confronted with otherwise. This week I talked about a paper published in Nature last Thursday about long lived Andreev-Floquet states in graphene Josephson junctions. It is a good reason for a blog about it.

The paper is: Steady Floquet-Andreev states in graphene Josephson junctions, from the group of Gil-Ho Lee at Postech, South Korea. Before starting with this paper, let me discuss Floquet states.

Take a free electron. It would be described by the Schrödinger equation and have a parabollic energy-momentum dispersion. If now you create a periodic lattice in space, the Bloch theorem tells you that you should get a band structure that is periodic in space. The underlying reason is that position and momentum are conjugate variables.

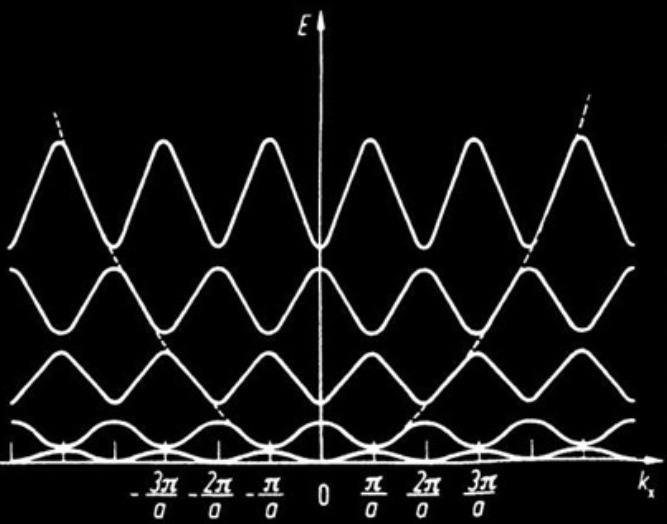
The Floquet states are analogues of Bloch states in the time domain. Since time and energy are conjugate variables, having a time periodicity in the system would result in a periodicity on the energy axis. In condensed matter systems, Floquet states were actually found using ARPES by the group of Nuh Gedik at MIT almost 10 years ago. The way they were observed was by irradiating a topological insulator with a short laser pulse and simultaneously observing the momentum-energy photoemission image. This shows a clear duplication of the band structure in energy: the Floquet states, but with two main drawbacks: a) the Floquet state exists for the time of the impulsion, a few femtoseconds; b) the laser pulse results in considerable heating of the sample.

Let’s now go back to the recent paper in graphene Josephson junctions. These Floquet states are based on Andreev bound states, that can be observed with tunneling spectroscopy as peaks in the dI/dV after the superconducting gap. By irradiating the graphene sample with a microwave excitation, in the same way that one would apply microwaves to observe Shapiro steps, the group of Gil-Ho Lee observed duplicate peaks at energies above and below the Andreev bound states. They characterised these states and provide a definitive proof of the Floquet nature through minute theoretical analysis. Interestingly, the separation between the Floquet states increases with the RF frequency and their number with the power. They also provide a Bessel function analysis (fig 2e) for these, but to me this is not convincing.

The strength of that paper lies in the fact that Floquet states could be found without heating the sample considerably (low frequency allow to use lower electric fields, therefore less heating) and graphene devices present good electron-phonon coupling, allowing continuous cooling in a dilution refrigerator. Additionally, these Floquet states are not volatile. In principle, nothing prevents them from disappearing. The authors claim that the states do not vary for 25h. In principle, this would allow further tuning of the band structure from microwave irradiations.