A week ago we published a paper in Nature physics showing the formation of van Hove singularities in twisted monolayer-bilayer graphene systems that can be tuned with the application of an electric field or by changing the twist angle. Notably, we show that these can cause strong correlations effects under various conditions. This is an interesting system, reproducing strongly correlated states seen in magic-angle graphene, but for some reason much easier to process.
Role of symmetry
Twisted van der Waals heterostructures usually offer different tuning parameters to create exotic state. In the case of twisted monolayer-bilayer graphene, there are more tuning knobs, compared to twisted bilayer graphene, because the band structure of multilayer graphene (here, bi-layer) is more tuneable than the one of the monolayer. Different stacking orders can exist for trilayer graphene: Bernal (ABA) or rhombohedral (ABC). The former presents a mirror symmetry and is semi-metallic, whereas the latter presents an inversion symmetry and is semi-conducting, with a gap that can be varied with the displacement field.
In twisted monolayer-bilayer graphene, the symmetry is even more reduced with the twist induced between the bilayer and monolayer graphene, that results in ABA-, ABB- and ABC-domains (cf schematic below).
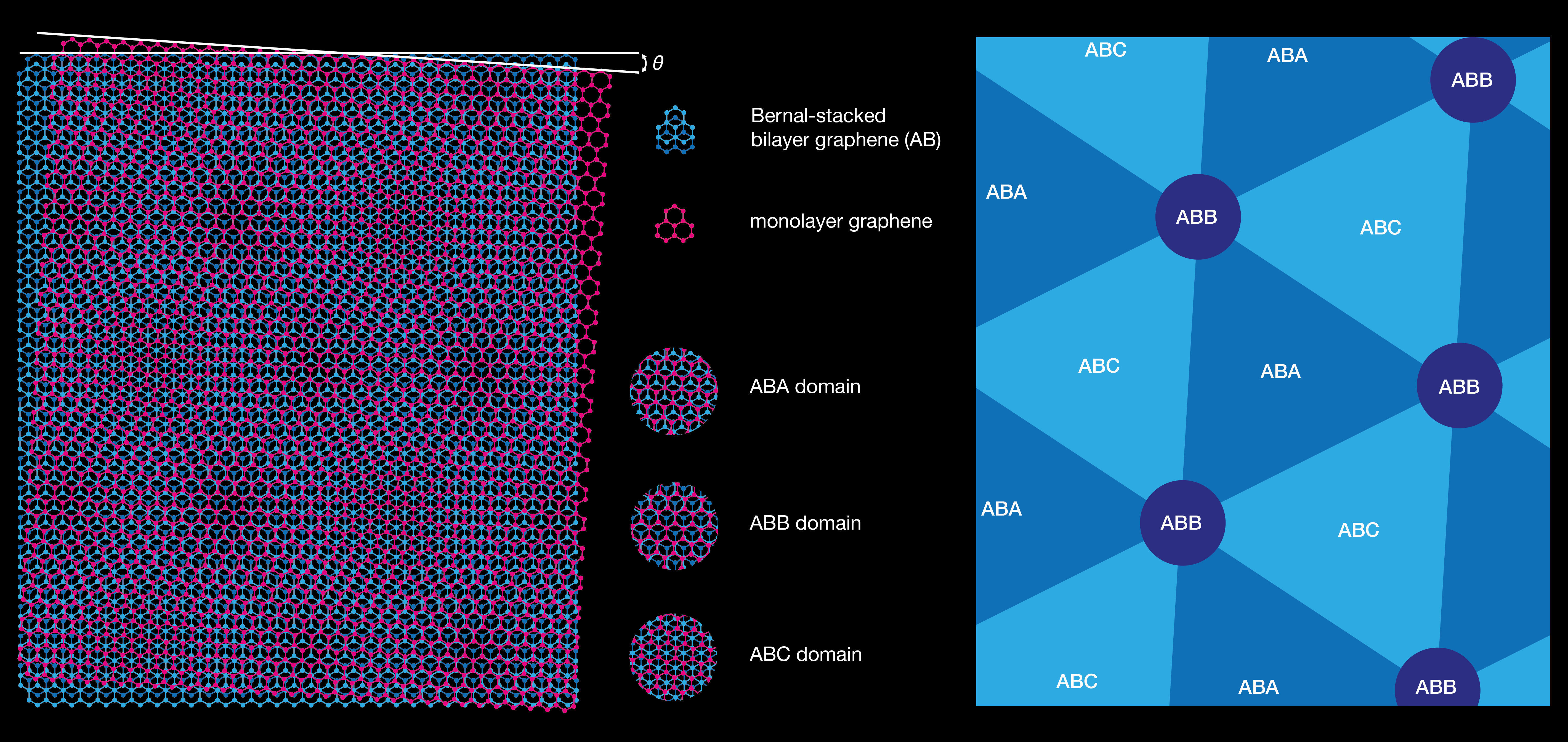
The phase diagram can be tuned via field-effect
In all the studies, twisted monolayer-bilayer graphene (tMBG) devices comprise a top- and back-gate, that allow to control the doping ($n$) or to apply a perpendicular electric field in the material ($D$).
Particularly, Chen et al have shown that a variety of correlated metallic, insulating and topological magnetic state appear, owing to the low symmetry. Particularly, the application of a displacement field endows this system with either the phase diagram of twisted bilayer graphene (at positive displacements) or twisted double bilayer graphene (at negative displacements).
We (Xu et al) have studied tMBG devices with a twist between 1.2° and 1.6° and studied the correlated states that appear asymetrically with the external electric field applied between the layer, and are highly tuneable by varying the twist angle. As shown on the following figure, two resistive peaks emerge at full filling $\nu = \pm 4$, and a gap opens at charge neutrality point (CNP) with increased $D$. The single particle model cannot explain the resistive and metallic states at half and quarter fillings. We have shown that the resistivity is asymmetric for electrons and holes in these states.
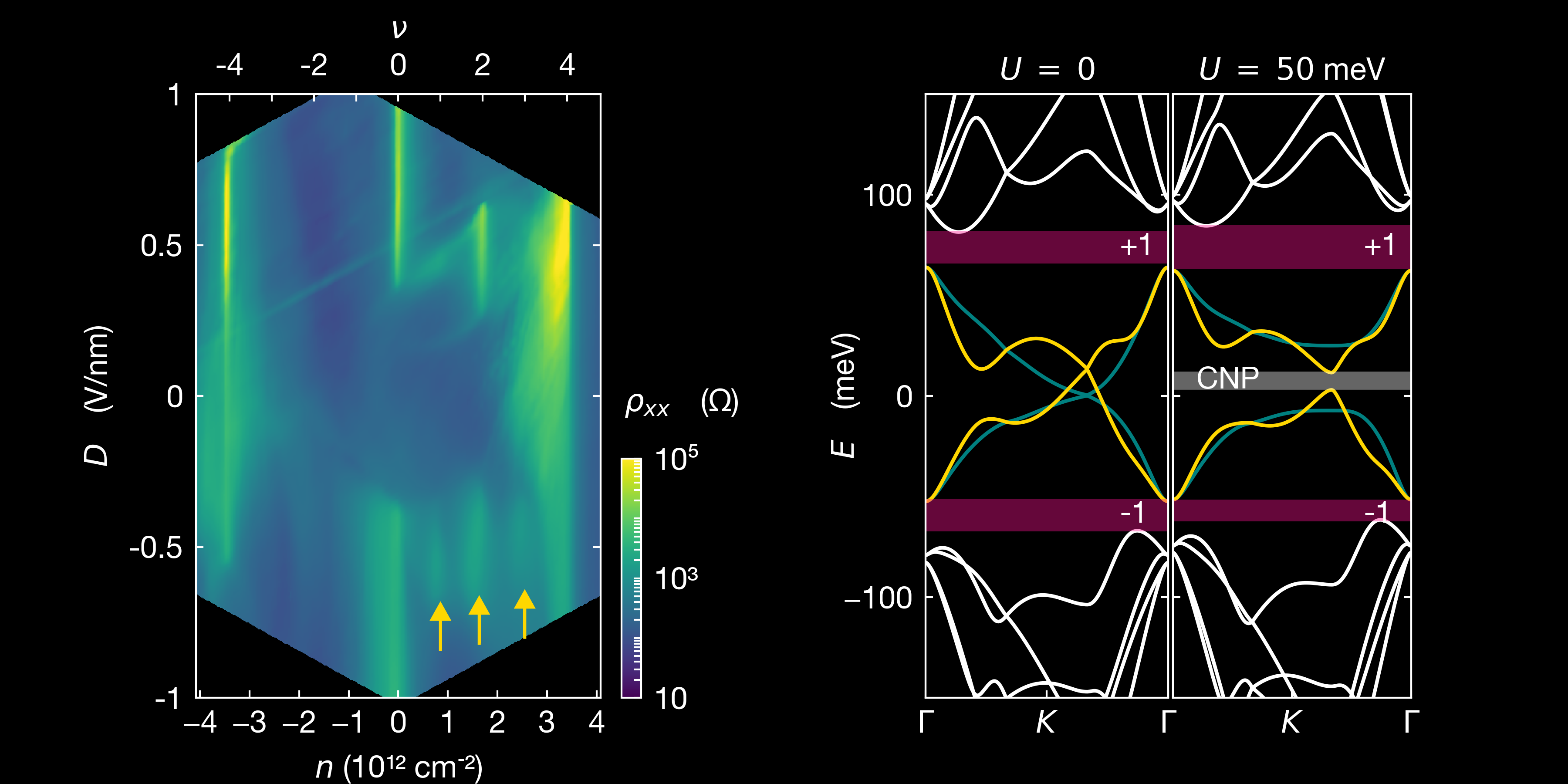
Correlated states at quarter filling
Polshyn et al have observed the correlated states corresponding to filling of 1 and 3 electrons per unit cell. In these states, they observe a quantised anomalous hall effect, with a transverse resistance close to $h/2e^2$. This could indicate a spontaneous polarisation of the system into a single-valley projected band. In the state with 3 electrons per unit cell, they show, as well, that the sign of the quantum anomalous hall effect can be reversed via field-effect control of the chemical potential. This is a major breakthrough.
Chen et al observe these correlated states undergoing an orbitally-driven insulating transition above a critical perpendicular magnetic field, for electric fields applied from the monolayer to the bilayer ($D>0$). Particularly, at $\nu = 1$ (one electron per moiré unit cell), they probe the emergence of an electrically tuneable ferromagnetism, in the conduction band, that is accompanied by an anomalous Hall effect.
More recently, He et al reported that orbital magnetism is abundant within the correlated phase diagram, leading to anomalous Hall states within the correlated metallic states around odd integer fillings of the flat conduction band. They also observe correlated Chern insulator that are stabilised within a magnetic field. Importantly, they show that this behaviour at zero electric field is inconsistent with simple spin and valley polarisation and propose an intervalley coherent state with an order parameter, breaking time-reversal symmetry.
All these study show that both electric and magnetic field can tune competition between correlated and topological phase, owing to the rich interplay between competing correlated states in twisted monolayer-bilayer graphene systems. So far, most of the recent study focused in the conduction band at $D>0$, where the system has a phase diagram comparable to twisted double bilayer graphene.
References:
- H. Polshyn et al 2020, Electrical switching of magnetic order in an orbital Chern insulator, Nature;
- S. Chen et al 2020, Electrically tunable correlated and topological states in twisted monolayer-bilayer graphene, Nature Physics;
- S. Xu, et al 2021, Tunable van Hove singularities and correlated states in twisted monolayer-bilayer graphene, Nature Physics;
- M. He et al 2021, Competing correlated states and abundant orbital magnetism in twisted monolayer-bilayer graphene.
 0000-0002-6484-2157
0000-0002-6484-2157