We just submitted the first first-author paper of my PhD, and uploaded on arXiv: “Long-range ballistic transport of Brown-Zak fermions in graphene superlattices”. (arXiv: 2006.15040) In this post, I highlight what we define as Brown-Zak fermions, and why their ballistic transport is important.

Brown-Zak fermions?

There is currently a huge interest in graphene superlattices and artificial stacks that can be obtained by crystallographic alignment of 2D crystals. Until now the community has mostly focused on additional gaps that appear in the Hofstadter-Wannier diagram. We believe that some attention should be directed towards the family of new metallic states that appear there. Particularly, the fermions appearing in rational fractions of the magnetic flux quantum have been eluded as “replica of Dirac fermions” (or described as “third-generation Dirac fermions”). This picture is ambiguous, as we show that these fermions are a different family of quasiparticles, that have a different spectrum as the Dirac fermions, and are described by a new quantum number.

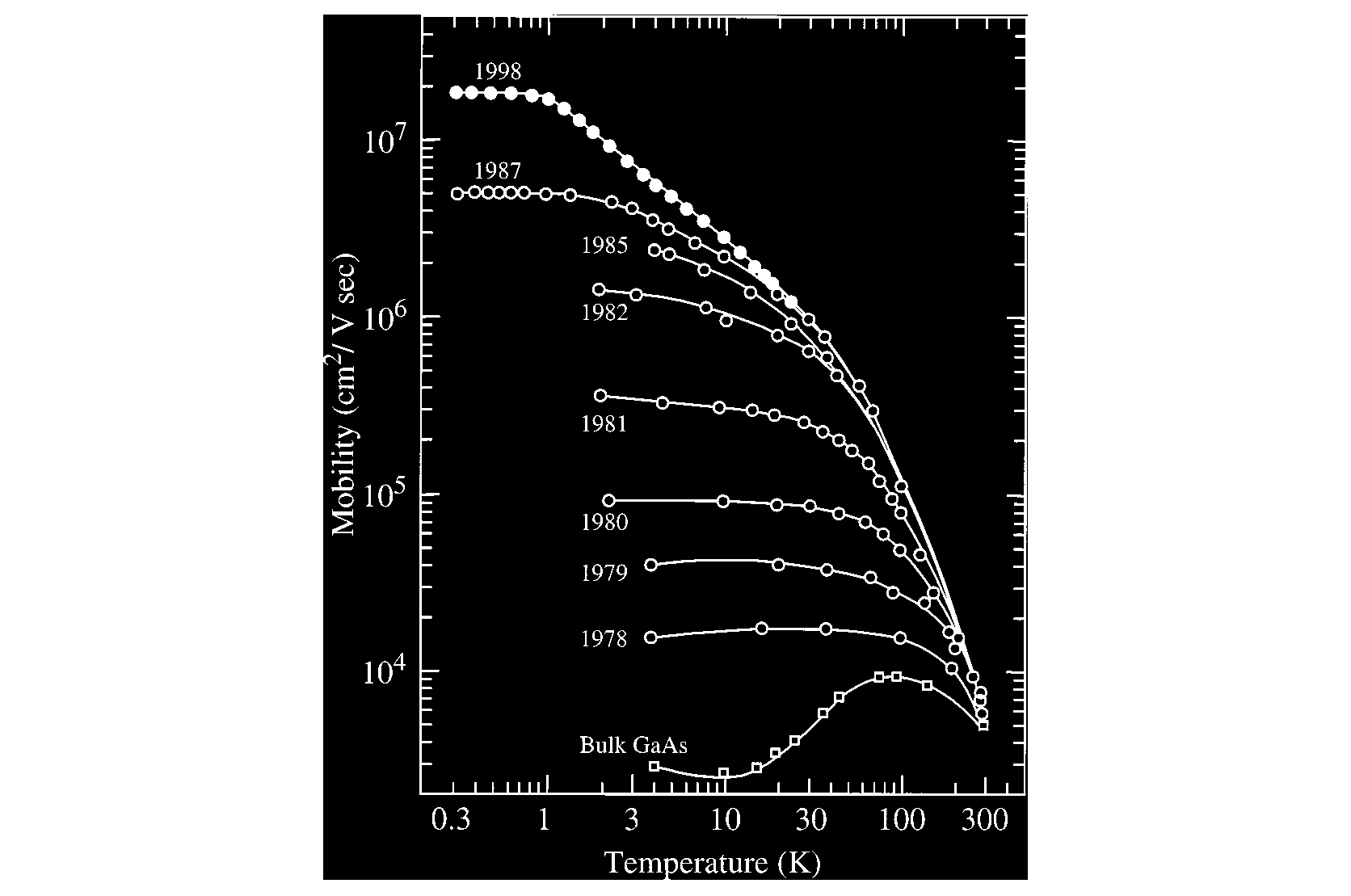
High mobility in 2DEG

In usual semiconductor 2DEG (e.g. GaAs/AlGaAs), the increase in device quality and induced electronic mobility have resulted in the discovery of a plethora of new effects. For example, the highest mobilities achieved in the early 1980s were about several thousands of cm²/Vs, that allowed the discovery of the integer quantum Hall effect (von Klitzing), and rapid increase allowed further phenomena to be observed, like the odd denominator fractional quantum Hall effect (Tsui, Stormer) and the even-denominator fractional QHE (Willet, Stormer) with mobilities about 10⁶ cm²/Vs. In general, new high-quality 2D electronic experimental systems with high mobility always deliver new physics.

Evolution of the best mobilities (μ) for GaAs/AlGaAs 2DEGs Picture extracted from Horst Stormer's Nobel lecture. At high temperatures, μ is essentially limited by phonon scattering, whereas at low temperature, the only limit is the concentration in impurities and defects.

Ballistic Brown-Zak fermions

In this paper, we report graphene superlattices of high quality, such as the Brown-Zak fermions exhibit mobilities above 10⁶ cm²/Vs, despite the presence of high magnetic fields, that always force conventional quasiparticles into curved cyclotron trajectories. This is comparable to the best values achieved for Dirac fermions in graphene devices or semiconductor 2DEGs. We demonstrate this in an ambiguous way (negative ballistic transfer experiment), proving that Brown-Zak fermions are Bloch quasiparticles propagating along straight trajectories.

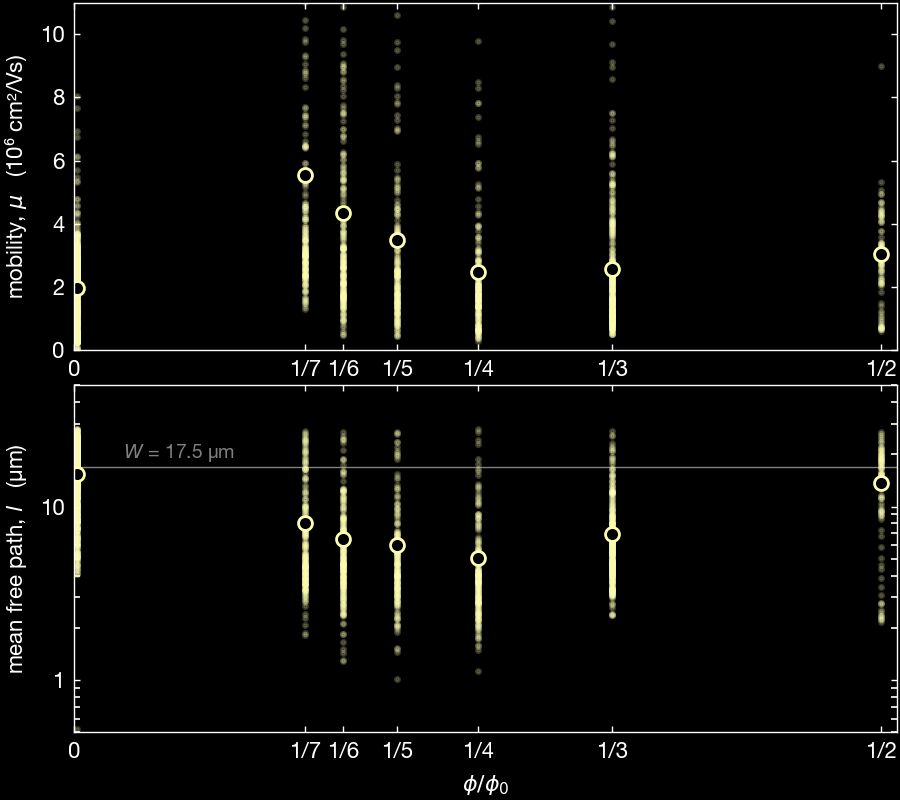
mobilities and mean free path for the family Brown-Zak fermions at fractions of the flux 1/q.

Additionally, the high quality of our superlattices allow us to get new information about the physics of Brown-Zak fermions. Particularly, we show that these quasiparticles are described by an additional quantum number q, that is the mini-valley degeneracy, and depends upon the attached fractions of the flux quantum. This comes over the spin and valley degrees of freedom from the main Dirac spectrum.

Finally, we show that at low temperatures, Brown-Zak fermions are strongly affected by electron-electron interactions. Hence, the classical single-particle Hofstadter model becomes obsolete, as it is too simplistic for the proper description of this family of new quasiparticles. The regime of strong interactions is also found to be full of strange effects, that we can only partially understand at the moment, such as bended fans ore staircase-like features.

In a nutshell, this work shows that Brown-Zak fermions can be seen as a new high-quality experimental platform to study unconventional quasiparticles (high-field but still Bloch-type). This should stimulate further experimental and theoretical work, with our paper showing the way.

References: