Metal halide perovskite present outstanding electronic properties. One hypothesis that explains those properties is the presence of a very strong bulk Rashba effect, reportedly the greatest among any other materials. This blog post introduces the Rashba effect in halide perovskites, explaining the origin of both the reported static and dynamic effects. Finally, I give some details about the theory from Byschkov & Rashba and about the photogalvanic effect.

Introduction

Metal halide perovskites (structure ABX₃ where X is a halide) have been subject to an unparalleled interest in the materials science community for the past 6 years. One reason for such an interest is their incredible long carrier diffusion lengths of up to 1 micron in polycrystalline films and as high as tens of microns in single crystals, driving outstanding photovoltaic performance. It has also been observed a strong optical absorption, with incredibly low non-radiative recombination rates, leading long carrier lifetimes — up to tens of microseconds. These parameters are surprisingly high for the unavoidable presence of defects in solution-processed polycrystalline films. This differs from the image of conventional semiconductors in which defects and impurities are responsible for scattering of carriers, lowering their lifetime and diffusion length.

Therefore, many fundamental questions underlying these outstanding optoelectronic properties still remain unanswered. Particularly, the origin of carrier mobilities, of long lifetimes and very low rate of non-radiative recombination need further studies. In fact, different hypotheses have been proposed to explain both the origin of long-carrier lifetimes and low rate of non-radiative recombination:

• The presence of a Rashba effect, from which an indirect band gap would originate;
• A considerably low density of deep intrinsic defects, each one having high formation energies;
• The existence of strong polaronic effects.

The Rashba effect would explain both the long carrier lifetimes and the intriguing low-rate of non-radiative recombination.

The Rashba effect in metal halide perovskites

Let’s start with the example of MAPI (perovskite phase where the A-site cation is methylammonium - CH₃NH₃, the metal, lead, and the halide is iodide), that is the most studied halide perovskite. In this structure, the presence of heavy atoms such as lead or iodine introduces spin-orbit coupling, that, along with inversion-symmetry breaking in the crystal, the electrons behave as if they were subject to an effective magnetic field which due to the spin-orbit coupling (SOC). This results in a momentum-dependent splitting of electron bands commonly referred to as the Rashba splitting. This effect yields a lifting of the degeneracy in k-space, inducing the shift of both the valence band (VB) maxima and conduction band (CB) minima, away from the high symmetry points of the Brillouin zone. This results in an indirect band gap, as shown in the figure below. Particularly, the splitting of the conduction band suppresses the rate of band-to-band recombination of charge carriers that has been proposed to be the origin of increased carrier lifetimes.

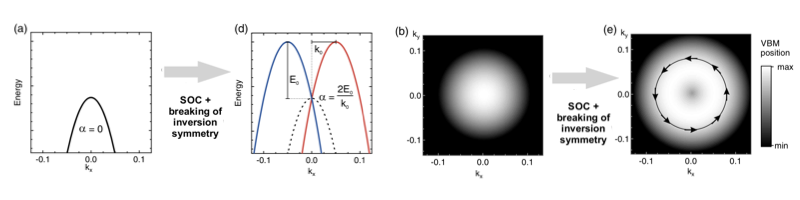
The inversion-symmetry breaking can happen either in the bulk of non-centrosymmetric crystals, or at surfaces and interfaces. It has been originally theorised for two-dimensional electron gases (2DEG, see below). There are two main mechanisms that lead to the Rashba effect, breaking the inversion symmetry in the bulk of the MAPI crystals, one is static, the other dynamic.

The static Rashba effect

First, lead iodide sub-lattice can distort from a set of ideal corner-sharing octahedra (tetragonal structure). As recently suggested (Rakita et al, PNAS 2017), this forms a non-centrosymmetric phase that is the source of the static Rashba effect. Particularly, the room-temperature of MAPI is the tetragonal I4/mcm phase, which is not centrosymmetric, that may not be subject to spin-splitting. In other phases, when the orbitals with spin-orbit splitting are not subject to inversion symmetry, the spin-orbit coupling causes a spin-dependent shift of the electronic bands along the k-direction. The double spin-degenerate band reportedly splits into two bands, shifted in k-space by k₀. Thus, the bandgap becomes slightly indirect, as the optical transition become spin-dependent. Particularly, these effects are responsible for a high Rashba parameter, whose intensity has been reported to be ɑ_R = 2 E₀ / k₀ = 7± 1 eV Å in the orthorhombic perovskite and  11 ± 4 eV Å in the cubic phase . These values are among the highest one ever reported

This effect on the optical transition can be probed with a photo-galvanic effect (see below), expected if coherent spin transport takes place on length scales large enough for spin-polarised currents to get through devices. That’s what Niesner and co-workers reported with their systematic study of the circular photo-galvanic effect in MAPI single crystals.

The spin-splitting also causes a minimum of energy at the central high symmetry point, of depth E₀. Particularly, in the room temperature tetragonal phase, they observed (Niesner et al, 2016) a circular photo-galvanic effect for excitations 110meV below the direct optical gap, indicating that the transitions between spin-polarised electronic bands happened below the direct gap.

Circular dichroism has also been observed in pump-probe spectroscopy, and spin dependence of the charge dissociation has been reported. This may allow for the creation of perovskite-based spintronic devices.

The dynamic Rashba effect

Recently, it has been proposed the existence of a dynamical Rashba effect, allowing for quantification of its magnitude. In fact, the cubic perovskite lattice allows high mobility of the organic dipolar cation that locally allow the breaking of inversion symmetry in the absence of any static distortion of the lead-iodide framework. Locally, this creates screening localisation domains that, combined with the presence of lead, provide MAPI with a giant SOC. The degrees of freedom of the molecular cation gives rise locally to a Rashba effect, fluctuating on the picosecond time scale, related to the dynamics of the methylammonium rotation. This shows that the Rashba effect exists in MAPI, regardless of whether the crystal lattice is centrosymmetric or not (i.e. is orthorhombic, tetragonal or cubic). Those dynamic structural fluctuations can occur as a result of the phonon modes or due to the interaction of the MA⁺ ions with the lead iodide framework.

Particularly, the soft nature of the lead-iodide bond allows it to be easily deformed under symmetry-breaking, due to the important fluctuation of the organic cations. At high temperature, this local structural disorder induces the dynamical Rashba effect.

The amplitude of this dynamical effect is very similar to the one that is observed for bulk Rashba systems (static Rashba). Hence, a change in the direction of the current, that is associated with the circular photo-galvanic effect at the orthorhombic-tetragonal phase transition, demonstrates that this dynamical effect has two different physical origins in the two phases.

At room temperature, the perovskite is tetragonal, thus the energy splitting between spin-polarised transition and direct optical transition increase with the temperature, as well as the amplitude of the circular photo-galvanic effect. Both effects are responsible for an increase of the Rashba parameter with the temperature, that has been measured experimentally (Niesner et al, 2018), giving support for the predicted dynamical Rashba effect.

The orthorhombic lattice is centrosymmetric. Hence, the bulk Rashba effect is impossible in this low-temperature phase. Thus the temperature-independent circular photo-galvanic effect that has been measured is attributed to the reduced symmetry at the surface and interfaces.

Finally, this Rashba effect explains the reported indirect-direct band gap and thermally activated radiative recombination in tetragonal MAPI (Hutter et al, Nature 2018). Particularly, this provides an evidence for the spin-splitting mechanism at elevated temperatures, that should be seen in materials with inversion symmetry that contains heavy elements like lead, and exhibit soft phonon modes.

Further applications

The Rashba mechanism described herein would potentially be very attractive for both optoelectronics and spintronics. Notably, the exploration of Rashba physics has now been at the heart of the growing research field of spin-orbitronics that focuses on the manipulation of non-equilibrium materials properties using SO coupling.

The reported Rashba effect in metal halide perovskites could pave the way towards new applications, thanks to the unique transport properties that emerge with such an effect. The tremendous field of spin manipulation using spin-orbit coupling could notably lead to a quantum spin Hall effect, to the possibility of creating spin-orbit Torque, spin-orbit Qubits or spin transistors or even study topological insulators and Majorana fermions…

I’m looking forward to reading papers involving halide perovskites in the fantastic field of spin manipulation. Given this, I now expect perovskite to have a pivotal role in modern physics with marvellous applications.

Appendices

About the Rashba spin-orbit coupling

In non-centrosymmetric crystals, the electronic energy bands are split by spin-orbit coupling. In those systems with structural inversion symmetry breaking, SOC becomes odd in momentum p, that, in two-dimensional electron gas (2DEG), reduces to a linear dependence of the Rashba effect in momentum.

For electrons moving in an electric field (even in the absence of external magnetic field), and effective magnetic field is felt by the electrons in their frame of motion. This is called the spin-orbit field, and couples to the electron’s magnetic moment. When inversion symmetry breaking is present, this SO field becomes odd in electron momentum. Let’s take the mathematical expression to better understand this:

Let’s chose an electron with momentum p moving across a magnetic field B. This electron experiences a Lorentz force in the direction perpendicular to its motion, F** = -e **p ×B /m and possesses a Zeeman energy μ_B σ·B, where σ is the vector of Pauli spin matrices, m the mass of the electron, e its charge, and μ_B is the Bohr magneton.

If this electron moves across an electric field E, it experiences the effective magnetic field B_eff ~ E × p /mc² in its rest-frame (c is the speed of light), and this field induces a momentum-dependent Zeeman energy called spin-orbit coupling, which Hamiltonian can be written Ĥ_SO~μ_B ( E × p )· σ /mc². In usual crystals, the electric field can be given by the gradient of the potential: E =- ∇ V. In quantum wells — that have structural inversion symmetry breaking, along the growth direction z — the spin subbands are split in energy. The band splitting was explained by Bychkov and Rashba considering an electric field E = E_z z resulting in an effective spin-orbit coupling of the form:

Ĥ_R = ɑ_R/ℏ · ( z × p ) · σ

Here, ɑ_R is the Rashba parameter. This formula has been derived for 2D plane waves and is only phenomenological, thus do not apply as such on real systems.

About the photo-galvanic effect

The spin of electrons and holes in solid state systems has been intensively studied in quantum mechanics and originates an outstanding number of phenomena. The dominant method to generate and investigate the spin polarisation has been optical orientation. Indeed, light propagation within a semiconducting material and scattering by inhomogeneities or mobile carriers is able to generate either a DC current (for short-circuit conditions) or a voltage (for open-circuit), that is called the photo-galvanic effect.

Under illumination with a circularly polarised light, it is possible to generate a transformation of the photon angular momentum into a translational motion of free charge carriers. To better understand this phenomenon, one can imagine it as the electronic analogue of a mechanic screw or wheel, that transform a rotation into a linear motion, respectively tangential or perpendicular to the rotation momentum). This effect has a strong signature due to this circular motion and leads to the possibility to produce helicity-dependent currents, whose behaviour upon the variation of the radiation helicity, the crystallographic orientation on the sample geometry, can be probed.

References:

• Etienne et al, JPCL 2016;
• Hutter et al, Nature Materials, 2017;
• Niesner et al, PRL, 2016;
• Niesner et al, PNAS, 2018;
• Rakita et al, PNAS 2017;
• Stranks et al, Nature Materials, 2018.